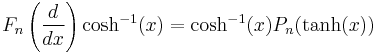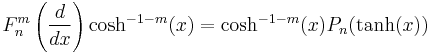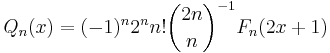Bateman polynomials
In mathematics, the Bateman polynomials are a family Fn of orthogonal polynomials introduced by Bateman (1933). The Bateman–Pasternack polynomials are a generalization introduced by Pasternack (1939).
Bateman polynomials are given by
where Pn is a Legendre polynomial.
Pasternack (1939) generalized the Bateman polynomials to polynomials Fm
n with
Carlitz (1957) showed that the polynomials Qn studied by Touchard (1956) are the same as Bateman polynomials up to a change of variable: more precisely
Bateman and Pasternack's polynomials are special cases of the symmetric continuous Hahn polynomials.
References
- Bateman, H. (1933), "Some properties of a certain set of polynomials.", Tôhoku Mathematical Journal 37: 23–38, JFM 59.0364.02, http://www.journalarchive.jst.go.jp/english/jnlabstract_en.php?cdjournal=tmj1911&cdvol=37&noissue=0&startpage=23
- Carlitz, Leonard (1957), "Some polynomials of Touchard connected with the Bernoulli numbers", Canadian Journal of Mathematics 9: 188–190, doi:10.4153/CJM-1957-021-9, ISSN 0008-414X, MR0085361, http://cms.math.ca/10.4153/CJM-1957-021-9
- Koelink, H. T. (1996), "On Jacobi and continuous Hahn polynomials", Proceedings of the American Mathematical Society 124 (3): 887–898, doi:10.1090/S0002-9939-96-03190-5, ISSN 0002-9939, MR1307541
- Pasternack, Simon (1939), "A generalization of the polynomial Fn(x)", London, Edinburgh, Dublin Philosophical Magazine and Journal of Science 28: 209–226, MR0000698
- Touchard, Jacques (1956), "Nombres exponentiels et nombres de Bernoulli", Canadian Journal of Mathematics 8: 305–320, ISSN 0008-414X, MR0079021, http://cms.math.ca/10.4153/CJM-1956-034-1